Randomized Numerical Analysis and its applications in Machine learnings
We focus on developing highly efficient, accurate, and statistically reliable Monte Carlo methods to compute complicated mutual interactions among extra large amount of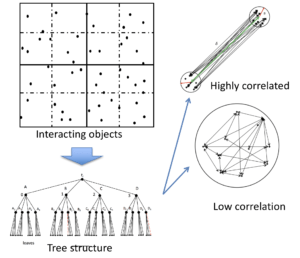 
objects. These algorithms are critical in the era of big data because any traditional, direct, brutal force methods for such problems are practically prohibitive even with modern computer power force. The mutual interactions of target objects are usually defined by kernel functions, which could represent physical kernels such as Green’s functions, mathematical kernels such as general integral operators, or statistical kernels used in kernel machine, kernel PCA, or kernelized Gaussian process regression. By using hierarchical structures, the global mutual interactions of objects are categorized into a sequence of local, but highly-correlated, or low-ranked interactions, which can be efficiently compressed, i.e., by randomly picking up a small amount of partial information, the major characteristics of the problem can be accurately captured at affordable costs. The data-oriented hierarchical structures, sampling algorithms, and the corresponding numerical/statistical analysis are our major research topics. These methods can be applied to study physical phenomena (such as electromagnetic interactions of charged particles in composite materials), biological problems (e.g. expression level of gene in experimental conditions in DNA microarray data), or even social sciences (digital social network).
Molecular biosciences
Macromolecules, such as RNA, DNA, or proteins are probably the smallest functioning units during all biological processes (if you don’t want to go to quantum mechanics). For example, VEGF is a small signaling protein secreted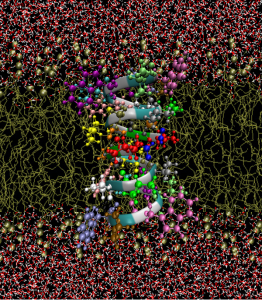 
by cells that restores oxygen supply to tissues when blood circulation is not sufficient. It can serve as a “good” role of creating new blood vessels during wound healing or a “bad” role of promoting angiogenesis of solid tumor. Another example could be ion channels, an important type of membrane proteins with holes that establish communications among cells and external environment. Functions of biomacromolecules heavily depend on their 3D structures, therefore, sophisticated multiscale models are necessary for balancing the detailed atomic structures of proteins and complicated solvent environment, as well as the dynamics of ionic flow.
My research along this line is based on the traditional implicit models such as Poisson-Boltzmann equation or Poisson-Nernst-Planck equations. Starting from variational principle, I am interested in developing multiscale models to study the complex dynamics of ionic flow through the extremely narrow channel pore. Mathematical problems may include how to describe accurate electrostatics near the solvent-solute interface, design of second-order interface methods for PDEs of elliptic type, and highly efficient and accurate numerical methods for quasi- and semi-linear elliptic equations.