Marvin J. Croy
Department of Philosophy
The University of North Carolina at Charlotte
Charlotte, NC 28223
mjcroy@email.uncc.edu
Abstract
A graphic means of representing deductive proofs in a sentential system of symbolic logic is presented. Proof construction is characterized as a domain of the cognitive theory of problem solving, and three different interface designs for supporting the working backwards method of proof construction are demonstrated. Following a description of the rule set and the working backwards method, an analysis is given of student performance data that has guided interface development during the past two years. One interface design is shown to be superior to the others in respect to working backwards. Finally, some general conclusions are drawn concerning the relevance of instructional programs for empirically documenting student difficulties and for improving interface designs.
Keywords: Proof Construction, Interface Design, Working Backwards, Graphic Interface, Problem Solving.
(This is a slightly edited version of an article which appeared in the Journal of Computers in Mathematics and Science Teaching, vol. 18, no. 4, 1999, pp. 371-386.)
Proof Construction and Problem Solving
The cognitive theory of problem solving defines a problem as consisting of three components: starting state, goal state, and operators (Newell & Simon, 1972). The operators provide rules of transition for legitimately moving from one state to another. The aim is to find an intermediate set of states, generated by the transition rules, which lead from starting state to goal state. Problem solving is thus characterized as a process of search which occurs within a problem space, the sum of all possible states which can legitimately be generated. This search is often guided by heuristic principles which select some states and paths of exploration as being more promising than others. This characterization of problem solving readily applies to the task of proof construction. In proof problems, the starting state is a set of symbolic expressions which constitute the problem’s given premises, and the goal state is a symbolic expression which constitutes the problem’s conclusion. The transition rules are formal rules of inference. The finished proof consists of a set of steps (states) which connect the premises to the conclusion, each step being an instance of a general rule.
These concepts have influenced the development of programs designed to facilitate the learning of proof construction. Proof construction involves a search through a complex set of alternatives, and recent programs supply a supportive environment for conducting and helpfully guiding that search. In particular, the ability to work simultaneously from premises to conclusion (working forwards) and from conclusion to premises (working backwards) is crucial (Scheines & Sieg, 1994). When engaged in working forwards from premises to conclusion, one searches for opportunities to apply rules, mainly by matching symbols in the problem’s given premise set to symbols in the premises of the rule set. Expressions thus produced may or may not be helpful in generating the problem’s conclusion, the goal expression. When engaged in working backwards from conclusion to premises, the focus is on the goal expression and what rule might generate it. Deciding this makes clear what the last step of the proof will be. This last step will involve a transition from some expression which serves as the starting point of an inference to the goal which serves as the end point of the inference. That starting point then becomes the new goal (sub-goal). This procedure can be continued so as to generate new sub-goals that when attained lead to the ultimate goal expression, the problem’s conclusion. The working backwards method has been shown to be an effective problem solving strategy in several domains (Anderson, 1990). In the present context, three interface designs have been developed as a means of exploring the working backwards method. Following a description of the rule set and the working backwards method, some data relevant to this method and the developed interfaces will be presented.
The Rule Set
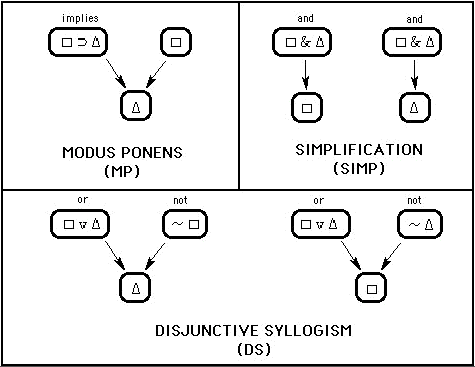
There are a variety of rule sets relevant to constructing proofs in sentential logic. The set to be discussed here consists of implication rules. This rule set is shown in Figure 1 and Figure 2.
Figure 1. Three Implicational Rules Serving the Function of Extraction
Figure 1 presents three rules: Modus Ponens, Simplification, and Disjunctive Syllogism. Rules are expressed in terms of geometrical shapes and logic symbols. The logic symbols represent truth functional connectives. The particular symbols used to define the rule set include for implication, ‘&’ for conjunction, ‘v’ for disjunction, and ‘~’ for negation. For the purpose of this exposition, the English meanings which most closely approximate these symbols are given outside of each oval containing a connective. (The first premise of Modus Ponens should be read as “square implies triangle.”) Geometrical shapes serve as variables which can be instantiated by particular expressions. The expressions substituted for these variables can be simple or complex. For example, an instance of Modus Ponens can be simple [ A B, A, therefore B ] or more complex [ (J&K) ~L, J&K, therefore ~L ]. Capital letters in these expressions can represent particular statements with a truth value of either true or false.
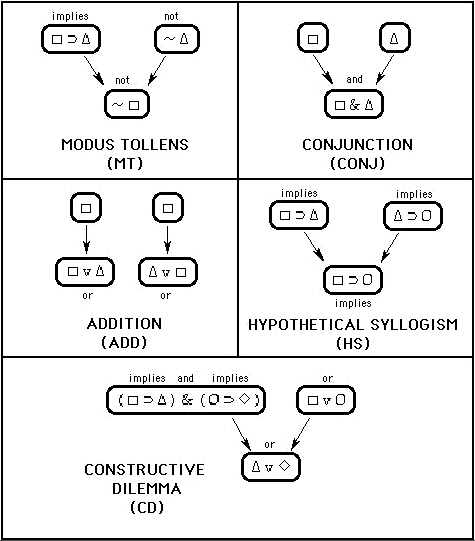
Each rule contains premise expression(s) and a concluding expression. Each expression is written inside of an oval, with premise expressions placed above and pointing to the concluding expressions which they generate. Each rule provides a deductively valid inference: the truth of the premise(s) guarantees the truth of the conclusion. Figure 2 presents five additional implication rules: Modus Tollens, Addition, Conjunction, Hypothetical Syllogism, and Constructive Dilemma. One key feature of these five rules is that each produces an expression which contains a logical connective. Modus Tollens always produces a negated expression, for example. The complex instance of Modus Ponens given above also produced a negated expression, and it is this sort of complication that makes accurate rule selection challenging. The working backwards method addresses this challenge by distinguishing between two general types of rule operations or functions. Each rule of implication performs either one of two functions: extraction or construction. Extraction occurs when the rule allows a subexpression to be generated from a larger expression. The extracted subexpression may be a simple letter or a more complicated expression. The rules shown in Figure 1 are extraction rules. By contrast, construction occurs when a rule generates an expression that is new in that it does not exist as a part of the expressions to which the rule is applied. The rules shown in Figure 2 are construction rules. When selecting a rule for producing a goal, it is helpful to first determine what kind of rule is called for in the given situation. This point will be elaborated below.
Figure 2. Five Implicational Rules Serving the Function of Construction
A Graphic Environment for Constructing Proofs
An effective interface for instructional programs makes essential conceptual distinctions perceptually clear. It is thus crucial in interface design to explicate the component tasks which comprise the problem solving enterprise and which must be successfully addressed for problem resolution. The interface should then provide a clear means for users to address those tasks. In proof construction these tasks center around the selection and appropriate sequencing of rule applications. Since this task can be approached in either a working forwards or a working backwards fashion, the interface should provide easily used mechanisms for applying rules and exploring paths in either of these directions.
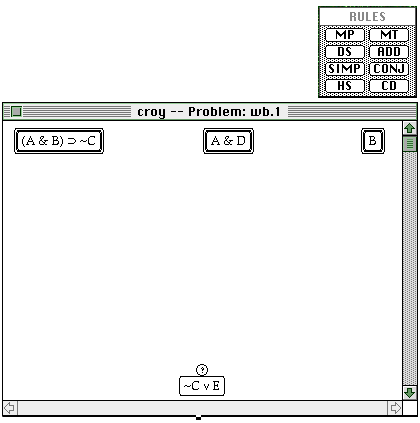
In other deductive systems such as geometry, graphical and symbolic representations have been helpful in the construction and understanding of proofs (Movshovitz, Shmukler, & Zavlavsky (1994); Schumann, 1991; Szymanski, 1994). The approach to be presented here employs a graphic representation of symbolic proofs in a sentential system of deductive logic. The program which incorporates this representation is named DEEP THOUGHT. It was built by the present author for the express purpose of collecting data on student proof construction efforts in order to identify particular patterns of errors (Croy, 1992; Croy & Amidon, 1991). Its role in providing helpful student feedback has previously been evaluated (Croy, Cook, & Green, 1993; Croy, Green, & Cook, 1995), but its working backwards mechanism has not previously been analyzed. The graphic representation used by DEEP THOUGHT is shown in Figure 3.
Figure 3. Graphic Representation of a Deductive Proof Problem
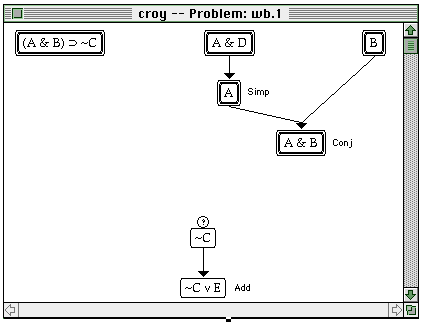
The logical expressions comprising the proof problem are displayed within oval nodes which are spatially distributed within a window. Premise nodes are placed at the top of the window while the conclusion node (indicated with a question mark) is placed near the bottom of the window. The intervening area constitutes the field of play in which the proof unfolds and is dynamically regulated to guarantee sufficient work space. To apply a rule top-down (working forwards), the student clicks on the node(s) containing the premise expression(s) which serve as the starting point of the inference and then selects the appropriate rule from a palette of rule buttons. Each button displays the abbreviation of a particular rule. Upon successfully completing this action, the program generates the resulting expression node comprising the end state of the transition. When working forwards, a rule selection can be erroneous on either syntactical or strategic grounds. Attempting to apply the rule Modus Ponens to the two leftmost premises in the problem in Figure 3, for example, would constitute a syntactical error. The general rule pattern does not fit the particular sequence of symbols in those expressions, and no concluding expression can possibly be generated by that attempt. The rule of Conjunction could, however, be applied to those two premises, but this application would constitute a strategic error since the expression generated would not help in arriving at the problem’s goal state. The DEEP THOUGHT program issues an error message in response to syntactical rule application errors, but not in response to strategic errors. Students must eventually determine for themselves that a dead end path has been pursued and must then recover and explore a more promising path. Figure 4 shows a proof in progress, with two steps made by working forwards and one step made by working backwards.
Figure 4. Graphic Representation of a Proof in Progress
The working forwards (top down) steps have applied the rules of Simplification and Conjunction. The working backwards (bottom up) step has selected the rule of Addition to produce the problem’s goal expression (‘~CvE’). When selecting a rule for working backwards, the first decision should be whether the goal expression is to be extracted or constructed. To decide this, the possibility for extraction should be investigated first. This is done by scanning the problem’s given premises, plus any expression already derived from them, to see if the goal expression exists as a part of one of these expressions. If so, a plan for extracting the aimed for subexpression can be formulated and evaluated. When this plan is judged to be infeasible, or the goal expression does not exist within the problem’s premise expressions or their derivatives, the goal expression should be produced by construction. In the present case, the goal expression (‘~CvE’) does not exist as part of any given or derived expression and hence must be constructed. One approach to support working backwards is shown as interface A below.
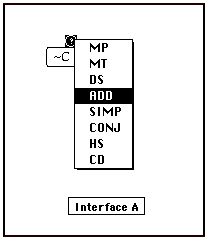When working backwards, the student clicks on the nodule containing the question mark which sits atop the goal expression node. Doing so pops open a menu that provides a list for rule selection. A correct choice from this list results in the display of the appropriate premise expression nodes for that step. As with working forwards, there are two types of incorrect working backwards rule choices. A working backwards rule choice can be syntactically incorrect if the rule cannot produce the connective structure of a particular goal expression. For example, the rule Modus Tollens always produces a negated expression and cannot produce the expression, ‘ A&B ‘. A rule choice can be strategically incorrect if the rule selected, while being one of several that can produce the syntactical structure of the goal expression, does not turn out to be the rule which ultimately does produce the goal expression. For example, the rules of Addition and Constructive Dilemma both produce disjunctive (‘or’) expressions, but only one of these might be appropriate in a given step. (This happens to be the case with the conclusion of the problem shown in Figure 4 where Addition is the best rule choice.) Interface A delivers an error message in response to syntactically incorrect working backwards rule selections but ignores strategically incorrect working backwards rule selections. As with working forwards, students must identify and recover from fruitless working backwards paths.
One initial concern about DEEP THOUGHT’s graphic representation of proofs concentrated on the working backwards facility. The question was whether student problem solving efforts would indicate that interface A was supportive. That is, would the use of the working backwards mechanism be frequent and successful? To answer this question, the program was coded so as to record each selection from the working backwards menu. One record of information was also collected for each selection from the working forwards rule palette. During the Fall, 1995, semester, 26 undergraduates enrolled in a sophomore-level, introductory deductive logic course were taught proof construction. The working backwards method was emphasized during in-class instruction, but working forwards was also explained. Students were assigned to complete at least three proof problems using interface A in DEEP THOUGHT. These problems ranged in difficulty in respect to the least number of steps required for completion. The simplest required at least three steps while the most complex required at least seven steps. (The problem shown in Figure 4 requires at least 4 steps.) This assignment produced a total of 3,018 rule applications, 1,105 while working forwards and 1,913 while working backwards. The rule application success rate for working forwards was 66% while that for working backwards was 51%.
These results provide little evidence for the effectiveness of the working backwards mechanism. While students did make use of the bottom-up approach more frequently than the top-down direction, a success rate of only 51% suggests that the feedback provided did not facilitate learning and/or that the interface components did not match well with the cognitive components of the working backwards task. This prompted an inspection of the working backwards rule selection errors. Two interesting findings emerged. To understand these findings, more needs to be said about the implication rule set.
The implication rule set does not emphasize the extraction-construction operations via the names of the rules, as is the case with some other rule sets. Consequently, the rules are often categorized in terms of the logical connectives which exist in the premise and/or conclusion of the rule’s formal definition. This categorization has its use in proof construction, but it should not be the immediate focus of attention for determining how to produce a goal expression when working backwards. Otherwise, errors which revolve around confusions over logical connectives are likely. As previously explained, the primary judgment to be made concerns extraction versus construction. The working backwards rule selection errors make it clear that students using interface A had difficulty making this judgment. Nearly half (46%) of the 935 errors are errors of this type. In these cases, not only was the inappropriate rule selected for working backwards, but the rule selected was not even the right type. A typical example involves the attempt to extract the subexpression ‘ A&B ‘ from the larger expression ‘ (A&B) C ‘. While this may look initially plausible, there is no rule which serves to extract the antecedent (left hand component) of a conditional expression. So, ‘ A&B ‘ must be constructed via the rule of Conjunction. This error delineates a general category of mistake: trying to extract what cannot be extracted. Another general category of mistake involves failure to extract what should be extracted. Students will sometimes fail to notice an opportunity to extract an expression and will instead endeavor to construct it. For example, when ‘ A&B ‘ is a goal expression, and ‘ (A&B)vC ‘ exists as a premise, students will sometimes try to construct ‘ A&B ‘ via Conjunction rather than first trying to extract it via Disjunctive Syllogism. These kinds of errors suggest that, when working backwards, students sometimes focus on the rule forms and their component symbols without first determining what type of rule is needed.
A second finding concerning the working backwards rule selection errors lends additional credence to this suggestion. One recurrent error pattern discovered involves the matching of the main connective in a goal expression to a main connective of a rule form’s premise expression. This relationship inverts the correct procedure. Correctly, the main connective in a problem’s goal expression should be matched to the main connective in a rule’s conclusion. For example, when trying to construct the expression, ‘AvB’, two rules are potentially applicable (Addition and Constructive Dilemma). Each of these rules produces a disjunction (‘or’) as the main connective of its concluding expression. By virtue of the match between the goal expression’s main connective and that of these rule forms, these are the only appropriate rules for producing this goal expression via construction. Sometimes, however, students select the rule of Disjunctive Syllogism instead. This rule contains a disjunction as a main connective, not in the rule’s conclusion, but rather in one of its premises. This kind of error occurred in 36% of the 935 working backwards rule selection errors made with interface A. Moreover, extraction-construction misjudgments and connective inversion errors appear to be closely related. When an error is an instance of an extraction-construction misjudgment, it is also an instance of a connective inversion in 47% of the cases. Given these data, two conclusions can be drawn. First, interface A did not provide a mechanism for working backwards that coincides with the component tasks. It did not encourage students to focus on the important tasks of determining extraction or construction. Second, this interface was in need of revision in ways that made the extraction-construction judgment much more explicit and active. Consequently, a revised version of the interface was designed.
The Design of Interface B
In order to encourage students to think of the transition rules in terms of their extraction-construction operations and to force an explicit choice between these operations, the working backwards mechanism of the interface was modified. The new interface, labeled B below, displayed two enabled options, ‘Extraction’ and ‘Construction’, in response to a mouse click inside the working backwards nodule (circled question mark). Moving the mouse cursor to one of these options popped open a sub-menu which listed the particular rules which serve that function. In the example below, the mouse button has been pressed while the cursor resides in the construction item, and hence the rules listed to the side constitute construction rule abbreviations. Moving the cursor through this list allows selection of a particular construction rule, in this case the rule of Addition. This design is intended to require selection of extraction or construction prior to selection of a particular rule.
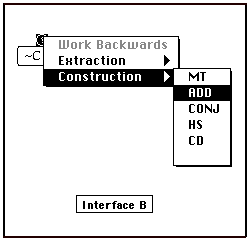Interface B was used by 26 students enrolled in Deductive Logic during the Spring, 1996, semester. As in the previous semester, the working backwards method was emphasized while working the same sequence of problems in class, and each student was required to work at least 3 proof problems from the same electronic problem set. The data generated by this activity consists of 2,849 rule applications, 1,873 while working forwards and 976 while working backwards. The working forwards rule application success rate was 74% while that for working backwards was 55%. Of the 924 working backwards rule selection errors, 45% involved erroneous extraction-construction judgments. Of this same group of 924 errors, 32% involved connective inversion mistakes. These results show little improvement over interface A. The overall working backwards error rate plus the rates concerning extraction-construction errors and connective inversions are at most within a few percentage points of those previously observed. Moreover, the data suggest that students did not much care for the working backwards mechanism. In contrast to interface A, working forwards operations are almost double the working backwards operations. The persistence of connective inversion errors is particularly bothersome. Interface B was designed to force students to make explicit extraction-construction choices which would initially focus attention on rule functions rather than the symbols embedded in goal expressions and rule forms. Neither of these objectives were achieved. In the face of these results, interface B appears to suffer a number of weaknesses. First, it is more complicated and perhaps burdensome than interface A. Second, its nested menu structure provides no feedback on the appropriateness of extraction-construction judgments. Finally, nothing prevents students from slighting the extraction-construction decision and focusing immediately on the rules themselves. By small movements of the mouse cursor through the Extraction-Construction options, one can peruse the rule abbreviations while giving little thought to the general rule functions. Doing this invites the same confusion concerning logical connectives in rule forms and goal expressions as was observed in the interface A data.
Data on working forwards steps were also analyzed. These data show that of the total 1,873 working forwards steps, 67% were syntactically correct and useful in generating the problem conclusion, 23% were syntactically incorrect, and 10% were syntactically correct but not useful in deriving the problem conclusion. Given these superior success rates, and the fact that students clearly preferred working forwards to working backwards, it seems that interface B made little progress toward implementing an effective mechanism for supporting the use of the working backwards strategy. Consequently, the interface was modified once again.
The Design and Evaluation of Interface C
The results reported above emphasize the importance of making sound extraction-construction judgments prior to selecting particular implication rules. Interface C was designed to separate these actions and to provide better feedback in response to errors. As shown below, interface C initially looked similar to the previous versions (stage 1). However, in response to a mouse click in the working backwards nodule, the menu which opened contained only two active options, ‘Extraction’ and ‘Construction’. No list of rule abbreviations was visible at this stage. Following this extraction-construction selection, a rule-choice dialog appeared off to the right (stage 2). Only then did students have an opportunity to make a rule selection. When errors were made, feedback was supplied relevant to each of these two decisions. In response to an incorrect extraction-construction judgment, students were warned that this selection did not appear tenable and were provided with a short explanation. At this point students could either cancel this operation or could continue on to make a rule selection. In response to an incorrect rule selection, students were informed that some other rule was required. As with previous versions of the program, students could construct fruitless paths of search which would ultimately have to be abandoned.
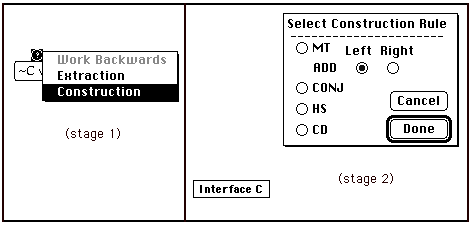This interface was used by two separate classes during the 1996-97 academic year. In-class instruction and assignments were the same as in previous semesters. The Fall, 1996, class of 30 students made a total of 2,365 extraction-construction judgments, 87% of which were correct. Of 2,016 working backwards rule selections made, 83% were correct. Among the incorrect rule applications, 12% involved connective inversions. There were 204 working forwards applications, of which 62% were correct. Results from 28 students during the Spring, 1997, semester were very similar. Of 1,749 extraction-construction judgments, 84% were correct. When selecting rules working backwards, correct choices were made in 79% of 1,434 cases. Connective inversion errors comprised 13% of the incorrect choices. Of 148 working forwards applications, 60% were correct. These results suggest that interface C was more effective than either of the earlier versions in respect to supporting the working backwards method. With interface C, most work was carried out working backwards rather than working forwards, and the respective success rates show that a greater proficiency was developed for working backwards. Interface C effectively separated extraction-construction judgments from rule selection decisions. By isolating the extraction-construction judgment and providing immediate feedback, students learned to make this key judgment with a high rate of accuracy. Doing so helped to prevent the occurrence of connective inversion errors.
To facilitate statistical comparisons of these results with those from the previous interface designs, error rates were calculated for each student on three variables. Table 1 presents mean scores for these variables from the three groups of students who used the different interfaces.
Table 1. Mean error rates for three working backwards interfaces, in percentages.
For the purposes of this analysis, the two classes using interface C are combined. (This procedure did not make any non-significant difference significant.) Statistical comparisons are made using unpaired, two-tailed t tests. The results of this comparison demonstrate no significant difference at the .05 level between interface A and interface B on any of the three variables. Significant differences do exist between the error rates of students using interface C and those using interface A and interface B. In respect to extraction-construction judgments, the error rates observed for interface C are significantly lower than those observed for interface A (t = 2.35, p = .02) and those for interface B (t = 4.46, p < .001). As for rule selection errors, the rates for interface C are significantly lower than the rates for interface A (t = 7.04, p < .001) and for interface B (t = 7.74, p = < .001). As for the percentage of rule selection errors which involve connective inversions, the percentages observed for interface C were significantly lower than those observed for interface A (t = 3.36, p = .001) and for interface B (t = 2.86, p = .005). These comparisons indicate that student performance using interface C for working backwards is clearly superior to that of students using interface A and interface B. Interface C thus appears to have made genuine progress toward implementing a mechanism which is congruent with at least some of the essential cognitive tasks involved in working backwards with sentential proofs. This progress should lay a foundation for further improvements. More needs to be discovered concerning the difficulties students have in learning sentential proof construction, and the DEEP THOUGHT program can play an important role in making those discoveries.
Conclusions and Implications
Working backwards can be a useful method in the context of sentential proofs with implication rules, and this method can be successfully learned by students given the proper support. That support should provide a clear separation of decisions concerning general rule function and particular rule selection. The interface described here was most effective when it made this conceptual distinction perceptually explicit.
The conclusions to be drawn from these efforts go beyond the issue of what constitutes a supportive environment for working backwards on sentential proofs. There is also something implied about the usefulness of instructional computer programs for gathering data whose analysis motivates, guides, and assesses pedagogical innovation. Such programs can provide windows on student difficulties which might otherwise go unnoticed. The occurrence of connective inversion in the present context, for example, would most probably have been undetected or underrated without the data collected by the proof construction program. More generally, instructional computer programs should be seen not merely as means for delivering instruction but also as means for improving pedagogical strategies and the interfaces which implement those strategies. To achieve this, the characteristics of students and their learning efforts need to be explored. By serving as observational devices, computers can facilitate this exploration and may eventually do for twenty-first century pedagogy what Galileo’s telescope did for seventeenth century astronomy.
Acknowledgments
This work was supported in part by funds provided by the University of North Carolina at Charlotte.
Jason Smith assisted in the collection and analysis of the data.
References
Anderson, G. (1990). Cognitive psychology and its implications, pp.219-254. New York, NY: W. H. Freeman and Company.
Croy, M. & Amidon, J. (1991). “A mouse-driven graphic interface for deductive proof construction,” in Burkholder, L. (ed.) Philosophy and the Computer, New York: Westview Press, pp. 198-203.
Croy, M. (1992). CAI to enhance human interaction in learning deductive proof construction, in 101 success stories of information technology in higher education: The Joe Wyatt challenge, pp. 501-506, edited by J. V. Boettcher. New York : McGraw-Hill, Inc.
Croy, M., Cook, J., & Green, M. (1993). Human versus computer feedback : an empirical and pragmatic study. Journal of Research in Computers and Education 27:185-204.
Croy, M., Green, M., & Cook, J. (1995). Assessing the impact of a proposed expert system via simulation. Journal of Educational Computing Research 13:1-15.
Newell, A. & Simon, H. (1972). Human Problem Solving. Englewood Cliffs, NJ: Prentice Hall.
Movshovitz, N., Shmukler, A., & Zavlavsky, O. (1994). Facilitating an intuitive basis for the Fundamental theorem of algebra through graphical technologies. Journal of Computers in Mathematics and Science Teaching 13 (3): 339-364.
Scheines, R. & Sieg, W. (1994). Computer environments for proof construction. Interactive Learning Environments 4(2):159-169.
Schumann, H. (1991). Interactive theorem findi Mathematics and Science Teaching 10 (3): 81-105.
Szymanski, W. (1994). Geometric computerized proofs = drawing package & symbolic computation software. Journal of Computers n Mathematics and Science Teaching 13 (4): 433-444.
About the Author
Marvin Croy has been designing and using computer programs to aid in the teaching of logic since his days as a graduate student at Florida State University. It was there that he took his Ph.D. in philosophy of science in 1979 and learned to design computer-assisted instruction programs on the PLATO system. After designing instructional programs on the PLATO system at Rutgers University on a project funded by Control Data Corporation, he began his teaching career at the University of North Carolina at Charlotte where he is currently an associate professor of philosophy. His work has mainly addressed the empirical and conceptual problems of using computers to achieve individualization, the design of graphic interfaces, and the general social and ethical issues surrounding the educational use of computers. His projects have been funded by The National Science Foundation, The National Endowment for the Humanities, and by The Foundation of the University of North Carolina at Charlotte.